Do you want to know the
optimal
economic value of your forest stand?
Do you want to know the optimal stock level in your forest stand?
Do you want to know how often you should harvest?
Do you want to know how changes in the parameters are affecting the optimal economic value and the optimal decisions?
Below, you find a java optimization program, F4, which you can use instantly over INTERNET in case you have Netscape 4.5 (or a later version) or Explorer 4.0 (or a later version). You press the button "Explanations", put the parameters which are relevant in your forest stand in the "boxes" and press the button "Optimize!". The optimal values and decisions are found directly below the buttons and the list of parameters. The optimization typically takes 0.1 seconds.
The program optimizes the present
value of all profits from the forest stand over an infinite horizon. The
optimal harvest pattern is determined by the harvest (thinning) interval
(years) and the minimum stock level. The parameters of the growth function,
the initial stock level, the rate of interest, prices and costs are specified
by you.
*Acknowledgements and Clarifications:
The author is grateful to Professor Mats Hagner who made the author explain one of the relations in greater detail. He pointed out that the function Growth = Growth(Volume) should be questioned. The author certainly agrees that the production is not a function of the volume as such. The trees certainly need "basic" inputs such as water, light and nutrients in order to grow well. If the trees have good access to light, water and nutrients, they grow well if they are healthy and have needles (leaves) of optimal quality and number (and ...).
Does the size of the trees affect the growth? In general, this should be expected. The number of needles and the competition in many respects (and many other conditions) usually change as the trees grow. We can often assume that a large and healthy tree grows more (totally) than a small tree. Perhaps it does not grow better per cubic metre than small trees. This is quite logical. Professor Hagner quite correctly pointed out that this is the case. Hence, the volume as such (of the stems) can not be expected to "explain" the growth. Professor Hagner commented that many small trees (with a total volume X) may grow better than a small number of very large trees (with the same total volume X). This is quite in line with the opinion of the author. The author however implicitly assumes that the relative frequencies of trees of different sizes are held constant. This has often been an assumption in "continuous harvesting models". But, as Professor Hagner stressed, it is important to mention this assumption.
Hence, after this acknowledgement with clarifications,
the author hopes that the ideas are more clearly stated and that the real
analysis can begin!
---------------------------------------------------------------------------------------------------------------------------
Now, you come to the java program F4!
In case you want to read more about the principles, see some references or complete examples, please move down to the headline "Background and Parameters" on this web page!
Background and Parameters
The model F4 optimizes the present value of all present and future profits from harvesting. The horizon is infinite. It is assumed that natural regeneration from the remaining trees (possibly helped by complementary plantation) dynamically gives the necessary number of new plants.
The volume (m3/ha) in the forest starts at a level V0, specified by the user.
The growth, G, (m3/(ha*year)) follows a logistic function:
G = sV(1-V/K)
where s = the "intrinsic growth rate" and K is the "carrying capacity". Please read Clark (1976) for a general background to these concepts.
r = the rate of interest in the capital market, P1 is the net profit in the initial harvest per cubic metre, P2 is the variable net profit per cubic metre in the future harvests and CS is the "fix cost" per harvest occasion and hectare (for instance including the cost of moving the harvester and the forwarder to the site and back).
The results
The optimal
present value is instantly found below the
parameter list. The optimal minimum volume
denotes
the optimal volume per hectare directly after each harvest. The optimal
harvest interval (is given in the unit "years")
and the optimal thinning volume
is the optimal volume harvested per occasion in the future.(Note
that the analysis is irrelevant in case "V0" < "Optimal Minimum
Volume".)
Empirical Background
A simple estimation of the logistic
growth parameters is found if you press
here! (The data comes from Lundqvist (1989). The regression estimate
of s is 5.4%.
From the regression results, we can determine the value of K,
which is 416
(m3/ha). It is interesting to observe that the coefficients are strongly
significant and that they have the expected signs. Forests
grow according to the same general principles as most other natural resources,
at least at this level of abstraction!
If you press
here, you get the graph of the growth function and the observations.
The real rate of interest, r, can be given the value 3% (in typical Swedish cases in the year of 1999). That is close to the real rate of interest if you invest in long term bonds. Of course, you should select the rate of interest which is relevant to your situation! (What is the best option you have to invest your resources over time? What rate of interest do you get then?)
P1, P2 and CS are strongly dependent on local conditions. We may, in some cases in Northern Sweden, assume that P1 = P2 = 200 (SEK/m3) and that CS = 500 (SEK/ha).
A complete example
1. Press the button "Explanations". Then, in the "boxes", explanations are printed. For instance, in the first box, you get this information: "1000*s". That means that you should write "54" in that box. (You should not write "", just 54 .) The reason why you select 54 is that s = 5.4% according to the empirical estimation shown above. In case you have some other value of s in your forest stand, please use the relevant figure!
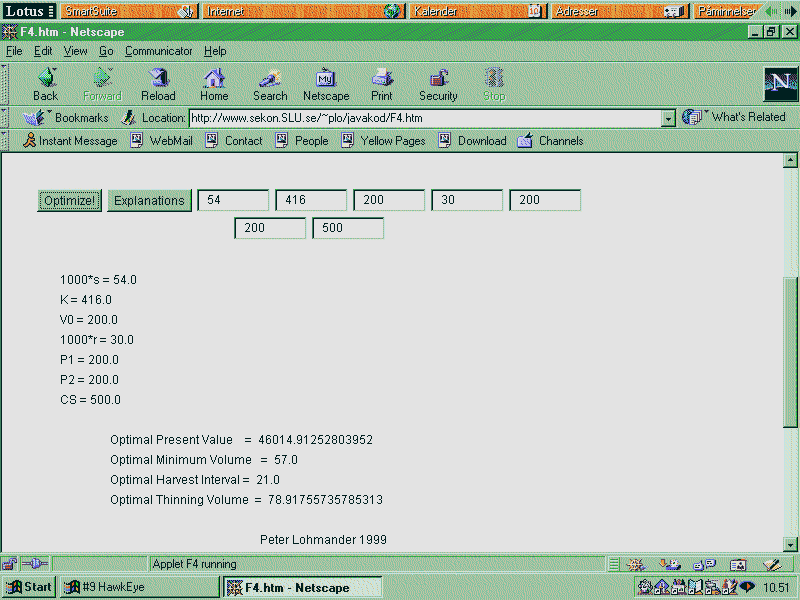
The picture (below) shows exactly what your screen should look like when you have written all the parameters in the boxes. (We assume that you initially have 200 m3/ha in your forest stand.) When you have done that, just press the button "Optimize"! All of the results are found on the same screen!

The results are all found
above. The optimal present value is 46 015 SEK/ha if you start with 200
m3/ha and follow the optimal program. You instantly harvest 143 (= 200
- 57) m3/ha. Then, you wait 21 years, harvest 79 m3/ha, (you go down to
57 m3/ha), wait 21 years again, harvest 79 m3/ha again etc. until the "end
of time"!
A complete second example
If we do not consider any costs associated with the transportation of harvesters and forwarders etc., we may assume that CS = 0. Then, we come to a more "classical" solution: We go to a stock level and stay there for ever! (See below!) (Note that the assumption of no machine transportation costs usually is irrelevant!)
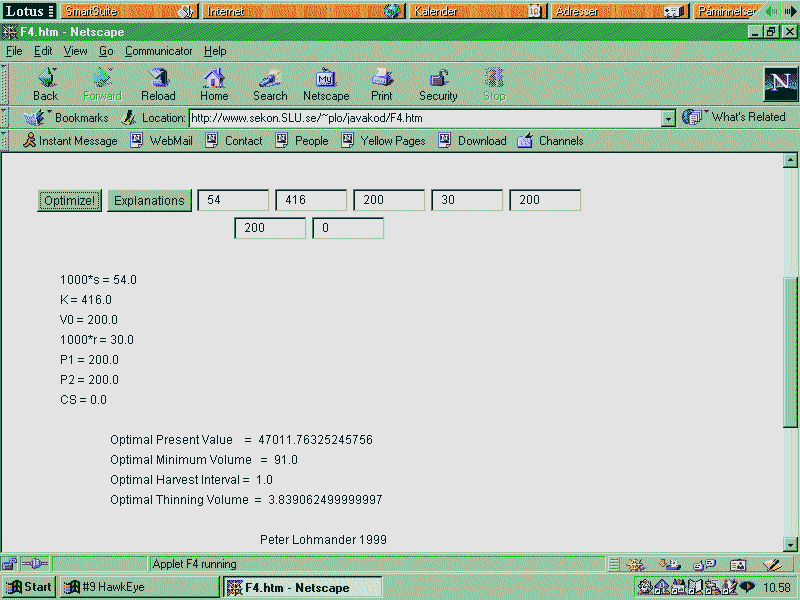
Now, you see that the optimal
decision is to harvest 109 ( = 200 - 91) m3/ha instantly and then harvest
the growth, 3.84 m3/(ha*year) each year. In other words, you come down
to the stand volume 91 m3/ha every year until "the end of time". The present
value is a little higher in this case than in the first case since CS is
lower.
Your own analysis:
Please change the parameters
and investigate how the results change! Test the alternatives which you
find to be the most relevant! How much should you cut? How often? What
is the economic value?
My very best regards,
Peter Lohmander
References
Some of the references essentially concern deterministic versions of the harvest problems and some concern stochastic versions of the same problems. If you are interested in stochastic versions of these problems too, which the author certainly hopes, please visit the home page of Peter Lohmander: http://www.sekon.SLU.se/~plo.
Clark, C.W., Mathematical Bioeconomics, Wiley, 1976
Hagner, M., Naturkultur som ett alternativ till det konventionella trakthyggesskogsbruket,
in
Lohmander, P., (editor), Analyses of economically optimal decisions at
a forest estate at the
coast of Västerboten in 1996, SUAS, Dept. of Forest Economics, WP-230,
1996
Hagner, Mats,
Lohmander Peter and Lundgren Martin, Computer aided choice of trees
for felling (Manuscript,
Submitted)
Jeansson, E., Ekonomisk analys av tre avverknings- och föryngringsalternativ
för bestånd nr
14 på fastigheten Kronören (Öresund 1:2), in Lohmander,
P., (editor), Analyses of
economically optimal decisions at a forest estate at the coast of Västerboten
in 1996, SUAS,
Dept. of Forest Economics, WP-230, 1996
Lindh, T., En ekonomisk jämförelse av kontinuerligt skogsbruk
och traditionellt
trakthyggesskogsbruk, in Lohmander, P., (editor), Analyses of economically
optimal
decisions at a forest estate at the coast of Västerboten in 1996,
SUAS, Dept. of Forest
Economics, WP-230, 1996
Lohmander, P., The economics of forest management under risk, Swedish University
of
Agricultural Sciences, Dept. of Forest Economics,Report 79, 1987 (Doctoral
dissertation) (Doktorsavhandling)
Lohmander, P., Continuous extraction under risk,
SYSTEMS ANALYSIS - MODELLING - SIMULATION, Vol. 5, No. 2, 1988
Lohmander,
P., Optimal resource control in continuous time without Hamiltonian
functions, SYSTEMS ANALYSIS - MODELLING - SIMULATION, Vol. 6, No. 6,
1989
Lohmander, P.,
A quantitative adaptive optimization model for resource harvesting in a
stochastic environment,
SYSTEMS ANALYSIS
- MODELLING - SIMULATION, Vol. 7, No. 1, 1990
Lohmander, P.,
Stochastic dynamic programming with multi-dimensional polynomial
objective function
approximations: - A tool for adaptive
economic forest
management, Swedish University of Agricultural Sciences, Dept. of
Forest Economics,
WP-120, 1990
Lohmander, P.,
Continuous harvesting with a nonlinear stock dependent growth
function and
stochastic prices: Optimization of the adaptive stock control function
via a
stochastic quasi-gradient
method, in: Hagner, M. (editor),
Silvicultural
Alternatives, Proceedings from an internordic workshop, June 22-25, 1992,
Swedish University
of Agricultural Sciences, Dept. of Silviculture, No. 35, 1992
Lohmander,
P., Economically optimal adaptive harvesting over time in the presence
of
economies
of scale in harvesting operations and stochastic markets, Proceedings from
the
general
biennial symposium of, Scandinavian Society of Forest Economics, May-June
1998
(The analysis
and the results were presented during the forest economic
excursion
of SSFE98) (In preparation)
Lundqvist,
L., Blädning i granskog, Strukturförändringar, volymtillväxt,
inväxning och
föryngring
på försöksytor skötta med stamvis blädning, SUAS,
Dept. of Silviculture,
Dissertation,
ISBN 91-576-3837-3, 1989
Ramade, F., Ecology of Natural Resources, John Wiley & Sons, 1984
Web sites with connected analyses:
http://www.sekon.SLU.se/~plo/dpmcln16.htm
http://www.sekon.SLU.se/~plo/rdnres1.htm
-------------------------------------------------------------------------------------------------------------------------------------------------------
Welcome to Peter Lohmander:http://www.sekon.SLU.se/~plo