Nuvex1
Nuvärde –
slutavverkningstidpunkt – exempel
Av
Peter Lohmander Version 2002-01-28
Här
ska vi se hur vi kan beskriva nuvärdet samt hur vi kan hitta den
slutavverkningstidpunkt som ger det högsta nuvärdet. Vi ska räkna ut värden i
en tabell och rita figurer.
Nuvärdet
av slutavverkningen inklusive markens värde – Några beståndsdelar:
Nuvärdet, som vi normalt vill göra så högt som möjligt, är uppbyggt av några olika delar som vi här ska titta närmare på. Allt detta kan vi själva räkna ut med hjälp av en vanlig räknedosa och vanliga skogliga tabeller. Det är viktigt att kunna göra detta själv så att man vet vad man gör och kan förklara detta för andra. Därför är det väsentligt att någon gång ibland se till att man kan räkna ut det som finns i denna text med hjälp av papper, penna och räknedosa. För dagliga kalkyler finns även datorprogram som löser detta snabbt. Då kan man direkt få en bestämning av den lämpligaste avverkningstidpunkten om man stoppar in aktuella förutsättningar i några tabeller.
Diskonteringsfaktorn:
Vi börjar med att titta på de delar som nuvärdet är uppbyggt av. Alla intäkter och kostnader måste justeras med hänsyn till när i tiden dessa infaller.
Om
vi får 100 SEK om ett år så motsvarar detta ett mindre värde än om vi skulle få
100 SEK redan idag. Pengarna måste diskonteras, d.v.s. multipliceras med diskonteringsfaktorn
för ett år. Diskonteringsfaktorn för ett år = 1/(1 + i) där i är den årliga
räntan. Om räntan i = 3% så blir diskonteringsfaktorn för ett år = 1/1.03 =
0.971 .
Detta
innebär att nuvärdet av att få 100 SEK om ett år = 0.971 * 100 SEK = 97.10 SEK.
Diskonteringsfaktorn
för tre år är (1/(1+i)) * (1/(1+i)) * (1/(1+i)) . Om räntan är 3% så blir diskonteringsfaktorn för tre år 0.915 .
Nuvärdet
av att få 100 SEK om 3 år är därför ca 91.50 SEK.
Man
kan också skriva diskonteringsfaktorn för tre år så här: (1/(1+i))^3.
På
samma sätt kan vi skriva diskonteringsfaktorn för ett godtyckligt antal år, t
år, så här: (1/(1+i))^t .
Virkesförrådet
per hektar:
Vi
antar att vi befinner oss i ett skogsbestånd med följande förutsättningar:
Just
nu finns 150 m3sk/ha. Tillväxten är 5 m3sk/ha/år. Därför kan vi beskriva
virkesförrådet så här:
Virkesförrådet
(m3sk/ha) = 150 + 5*t
Nettopriset
per m3sk:
Vi
räknar ut timmerandel och massavedsandel i beståndet och gör en
kvalitetsbedömning. Vi beräknar drivningskostnad och får fram ett nettopris per
m3sk som gäller just nu. Nettopriset just nu är 190 SEK/m3sk.
Vi
tänker oss därefter att vi lämnar beståndet och kommer tillbaka om 5 år. Vid
den tidpunkten finns ett högre virkesförråd. Timmerandelen och massavedsandelen
har antagligen ändrats något. Timmerkvaliteten har möjligen ändrats. Eventuellt
har andelen träd med rotröta ökat. Drivningskostnaden per m3sk har antagligen
sjunkit något. Vi räknar ut ett nytt nettopris per m3sk som gäller om fem år. Vi
antar att detta blir 195 SEK/m3sk.
Vi
konstaterar därefter att nettopristillväxten är 1 SEK/m3sk/år. (195–190)/5 = 1.
Därför
kan vi beskriva nettopriset så här:
Nettopris
(per m3sk) = 190 + 1*t
Markvärdet
per hektar:
Markvärdet
efter slutavverkning är 2000 SEK/ha. Detta värde kan räknas ut på olika sätt. Om
detta värde ska beräknas helt korrekt krävs separata utredningar i varje
enskilt fall. Just i detta aktuella problem är det för det mesta inte avgörande
att vi har absolut rätt markvärde. En typisk siffra i mellersta Norrland ligger
i intervallet 0 SEK – 2000 SEK.
Nuvärdet
per hektar:
När vi nu känner till de delar som nuvärdet är uppbyggt av kan vi skriva nuvärdet så här:
Nuvärde = (1/(1+i))^t * ( (190 + 1*t) * (150 + 5*t) + 2000)
Vi
kan tillverka en tabell (Se Tabell 1.) och där skriva ner diskonteringsfaktorn,
virkesförrådet (volymen) per hektar, nettopriset samt markvärdet och nuvärdet för
olika år (T).
Den
bästa slutavverkningstidpunkten:
Vi
kan med hjälp av Tabell 1. bestämma högsta möjliga nuvärde. Detta får vi om vi
slutavverkar om 10 år. Om vi skulle ha tillverkat en mer detaljerad tabell (och
låtit varje möjligt år representera en rad) så skulle vi ha funnit att det vore
ännu bättre att avverka om 8 år med dessa förutsättningar.
Vi
kan också med hjälp av Tabell 1. i
grova drag räkna ut hur mycket vi skulle förlora i nuvärde, i jämförelse med
bästa alternativ, om vi väljer att slutavverka vid andra tidpunkter än den
bästa. Denna skillnad i nuvärde kallas vanligen inoptimalförlust. Om vi tror på
siffrorna i Tabell 1. så är inoptimalförlusten 751.94 SEK/ha om vi avverkar
omedelbart istället för vid den bästa avverkningstidpunkten (enligt tabellen). (Om
vi skulle ha haft en mer detaljerad tabell så skulle vi ha kunnat göra mer
exakta beräkningar.)
Tabell
1.
(Förklaringar i texten.)
|
T |
Disk.faktor |
Volym |
Nettopris |
Markvärde |
Nuvärde |
|
-10 |
1,34 |
100 |
180 |
2000 |
26878,33 |
|
-5 |
1,16 |
125 |
185 |
2000 |
29126,76 |
|
0 |
1 |
150 |
190 |
2000 |
30500 |
|
5 |
0,86 |
175 |
195 |
2000 |
31161,74 |
|
10 |
0,74 |
200 |
200 |
2000 |
31251,94 |
|
15 |
0,64 |
225 |
205 |
2000 |
30889,61 |
|
20 |
0,55 |
250 |
210 |
2000 |
30175,33 |
|
25 |
0,48 |
275 |
215 |
2000 |
29193,64 |
|
30 |
0,41 |
300 |
220 |
2000 |
28015,1 |
|
35 |
0,36 |
325 |
225 |
2000 |
26698,18 |
|
40 |
0,31 |
350 |
230 |
2000 |
25290,94 |
|
45 |
0,26 |
375 |
235 |
2000 |
23832,53 |
|
50 |
0,23 |
400 |
240 |
2000 |
22354,49 |
Den
bästa slutavverkningstidpunkten via ett diagram:
I
Figur 1. ser vi hur vi kan rita ett diagram över nuvärdet för olika
slutavverkningstidpunkter. Jämför uppgifterna i Figur 1. med uppgifterna i
Tabell 1.
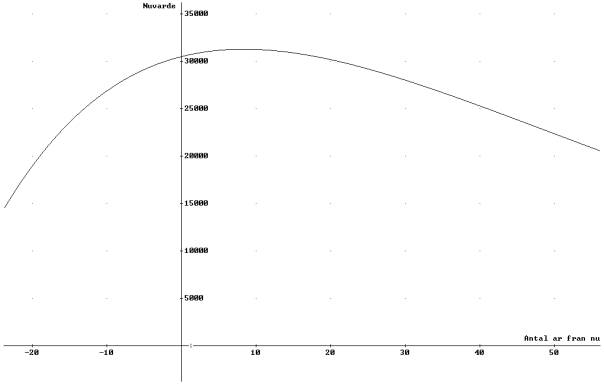
Figur
1.
Nuvärdet
av beståndet (inklusive markvärdet) som funktion av slutavverkningstidpunkten,
t. Kalkylräntan är 3%.
Nuvärde = (1/1.03)^t * ( (190 + 1*t) * (150 + 5*t) + 2000)
Hur
påverkas den lämpligaste slutavverkningstidpunkten av kalkylräntan?
I Figur 1. – 3. ser vi hur den optimala slutavverkningstidpunkten påverkas av kalkylräntan. När kalkylräntan är hög så bör vi avverka tidigare än om kalkylräntan är låg.
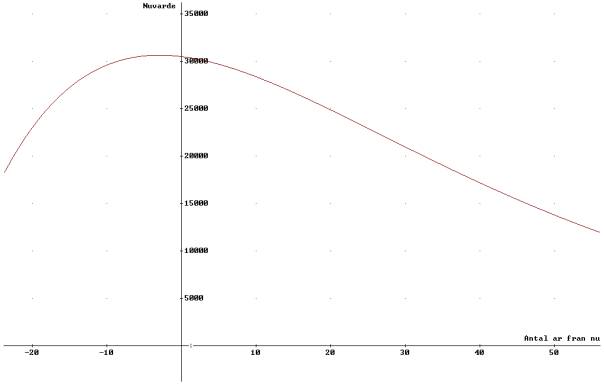
Figur
2.
Nuvärdet av beståndet (inklusive markvärdet) som funktion av slutavverkningstidpunkten, t. Kalkylräntan är 4%.
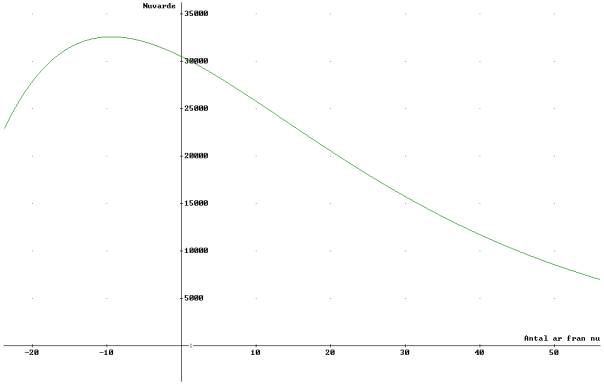
Figur
3.
Nuvärdet av beståndet (inklusive markvärdet) som funktion av slutavverkningstidpunkten, t. Kalkylräntan är 5%.
Viktiga
observationer:
Den
skogsägare som har en hög kalkylränta, exempelvis en skogsägare som har ett
högt belånat hus med hög ränta på villalånet, borde ha avverkat skogsbeståndet
för flera år sedan. Skogsägaren borde ha betalat av på lånet redan då.
En
annan skogsägare som inte har några lån alls har kanske 3% kalkylränta. En
sådan skogsägare bör inte avverka detta skogsbestånd nu utan vänta ytterligare
ca 8 år.
Det är viktigt att komma ihåg att dessa beräkningar inte har tagit hänsyn till prisvariationer, begränsningar i skogsvårdslagen och andra speciella förhållanden. Det finns särskilda beräkningsmetoder och datorprogram som även kan ta hänsyn till sådana fenomen.